Introduction to GraphQL
GraphQL is a query language.
See the quick introduction in the docs but, essentially, we are working with
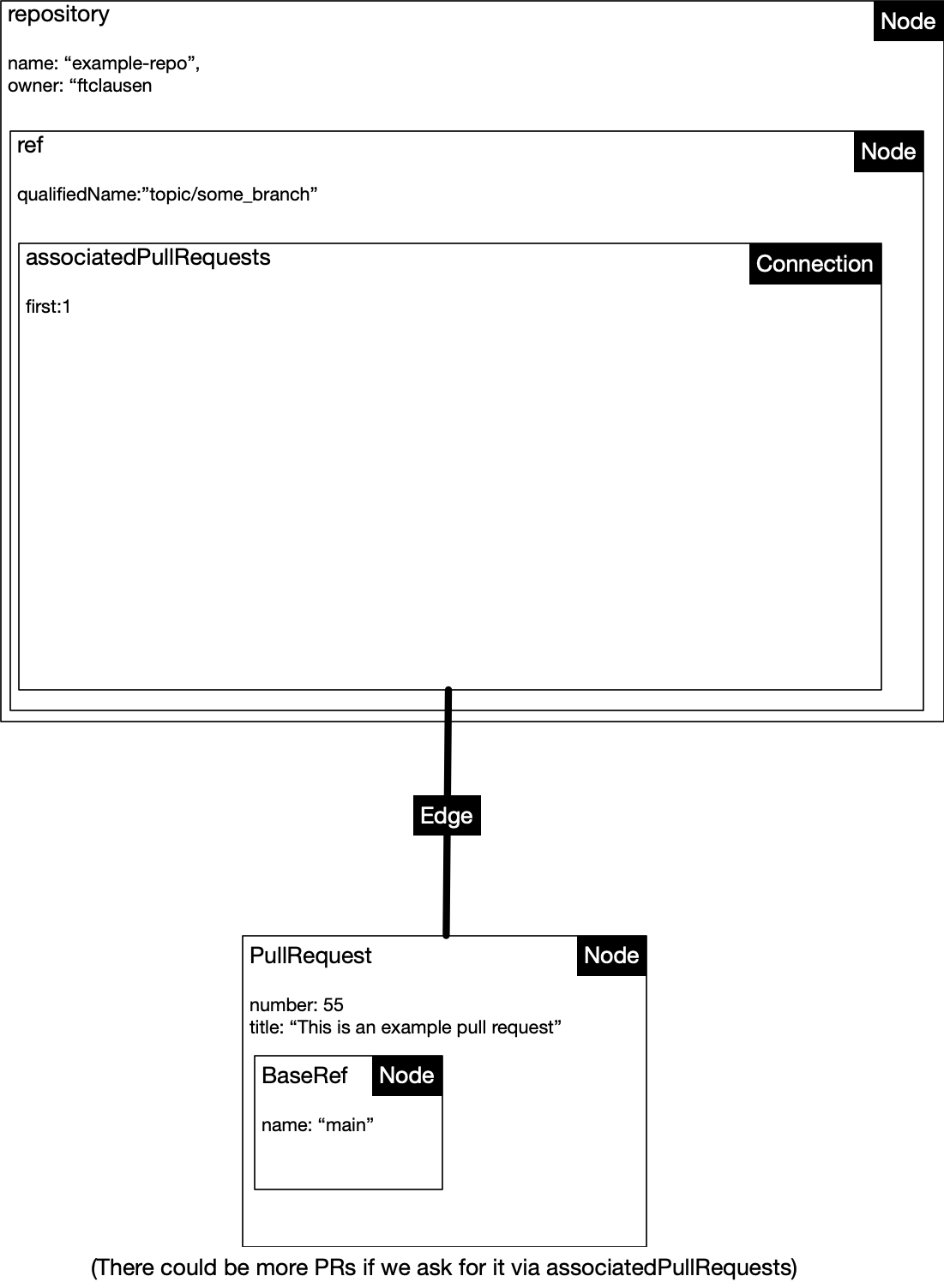
- Connection: Like SQL these let you query related objects in the same call. E.g.
associatedPullRequestsis a connection between a branch (ref) and a pull request. - Nodes: Generic term for an object. We are interested in the
pullrequestobject - Edge: Represents connections between nodes e.g. pull request(s) that are associated with a PR
Here is the query we are using to find which PR(s) are associated with a given commit (only using the first one found so far):
{
repository(name: "example-repo", owner: "ftclausen") {
ref(qualifiedName:"topic/some_branch") {
associatedPullRequests(first: 1) {
edges {
node {
number
title
baseRef {
name
}
}
}
}
}
}
}
This then returns the following data
{
"data": {
"repository": {
"ref": {
"associatedPullRequests": {
"edges": [
{
"node": {
"number": 55,
"title": "This is an example pull request",
"baseRef": {
"name": "main"
}
}
}
]
}
}
}
}
}
As best I understand edges will always be an array. Finally this can be imagined graphically which I find useful:
We then pull the above data in and use it as needed
How to represent types for GraphQL data
Given GraphQL data varies per type I followed this very helpful guide guide to generate types for GraphQL responses instead of manually doing it. Please see that for a concrete example.
A note on the concept of a Pull Request
We have three different ways pull requests are represented depending on the context:
- Pull Request Event: When a new PR is created we get a pull_request event payload
- REST API Pull Request response
- Pull Request from GraphQL response
So that is something to be aware of when working with TypeScript. I had to make my own meta-object to unify this for my purposes; this meta-object extracted just what I needed out of each one of the above types.
]]>