How to Solve It - Chains of Auxilliary Problems
This is from George Pólya’s “How to Solve It” book. I am reading this because I want to sharpen my problem solving skills and, eventually, be able to make derivations like this in Concrete Mathematics.
In How to Solve It they go through a series of equivalent problems to find the eventual solution. So we may not know the solution to our original problem A but we can go through B, C, D, etc. until we find a solution we know or that can be directly “seen”.
The book goes through solving this equation with the unknown $x$
\[x^4 - 13x^2 + 36 = 0\]Since I am bootstrapping my mathematical knowledge I found the book’s treatment a bit terse without many explanations of how they got to each step. I eventually figured out that they are trying to massage the equation into a state where you can apply the perfect square rule. This makes things much simpler to reason about and thus find the solution.
Step A - The original equation.
As mentioned above this is
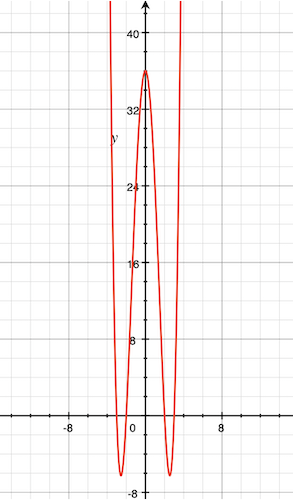
\[x^4 - 13x^2 + 36 = 0\]And our task is to find $x$. Or, more specifically, where the graph intercepts the $x$ axis at $0$. The steps are essentially a set of quadratic equation equivalence conversions.
Step B - Multiple by powers of two
My slow self needed to ponder this one for a while. In any case, B ends up being
\[(2x^2)^2 - 2(2x^2)13 + 144 = 0\]This had me baffled for a while but I, eventually, saw that they are multiplying by increasing powers of two. I don’t know if this technique has a name or how they arrived at doing this first step but, to write it another way,
\[\begin{align} 2^0\cdot(2x^2)^2 - 2^1\cdot(2x^2)13 + 2^2\cdot36 &= 0 \\ (2x^2)^2 - 2(2x^2)13 + 144 &= 0 \end{align}\]Step C - Add 25 to each side
For those who know quadratics quite well can probably see where they are going with these steps but, anyway, I was still baffled at this stage but at least it could see the manipulation easily enough:
\[\begin{align} (2x^2)^2 - 2(2x^2)13 + 144 + 25 &= 0 + 25 \\ (2x^2)^2 - 2(2x^2)13 + 169 &= 25 \end{align}\]Step D - Make it short!
This makes things much more compact through, as I eventually figured out, the perfect square rule! To remind the forgetful like me it is: $(a - b)^2 = a^2 - 2ab + b^2$. There is also a $a + b$ version.
\[\begin{align} (2x^2)^2 - 2(2x^2)13 + 169 &= 25 \\ (2x^2 - 13)^2 &= 25 \end{align}\]The more compact form gives us a better handle on things. This is a key step to solve this more easily. The following steps are using this step to find the four solutions.
Step E - Partial “solution”
Here we take the square root and find a sort-of solution that still needs some work. Let’s call it the IKEA solution:
\[\begin{align} (2x^2 - 13)^2 &= 25 \\ 2x^2 - 13 &= \pm5 \end{align}\]Step F - Re-arrange
Let’s isolate the $x^2$ like it has covid:
\[\begin{align} 2x^2 - 13 &= \pm5 \\ x^2 &= \frac{13\pm5}{2} \end{align}\]Step G - Almost there!
Now we take the square root remembering our $\pm$:
\[\begin{align} x^2 &= \frac{13\pm5}{2} \\ x &= \pm\sqrt{\frac{13\pm5}{2}} \end{align}\]Step H - The answers!
Now can see what the concrete answers are: $x = 3$ or $-3$ or $2$ or $-2$.